MUM-based hash functions
I have had a long-standing interest in hash functions. This interest
naturally grew out of my 40 years of work on compilers and various
programming language processors. The reason is simple: the most
efficient universal search–insert-delete data structure in compilers
is the hash table. Although hash table can have a quadratic
complexity in the worst case, in practice it outperforms any
n*long(n) complexity data structure, such as different balanced
trees.
Earlier in my career, I devoted considerable attention to designing fast hash tables, and I achieved some success in this area. For example, my hash tables are used in GCC and Ruby.
Once you already have a good hash table implementation, the choice of hash function significantly affects its performance. That is why, in recent years, my interest has shifted toward the design of efficient hash functions for hash tables.
Criteria for a good non-cryptographic hash function
Hash functions are generally divided in two categories: cryptographic and non-cryptographic. The latter are typically used in hash tables. Throughout this discussion, when I mention “hash function” I mean non-cryptographic hash functions.
Here are my criteria for good hash functions, listed in order of importance:
-
Speed. Unlike cryptographic functions, speed is the top priority, since it is critical to the overall performance of the hash table. A good hash function should also be fast for short keys. For example, in optimizing compilers, the key length for performance-critical hash tables is often just a few machine words. In non-optimizing compilers, typical hash functions are applied mostly to strings and identifiers, whose lengths range from a few bytes to a few dozen bytes. By contrast, cryptographic functions are often applied to large amounts of data, such as entire files.
-
Quality. To keep the complexity of hash table operations linear, the hash function results must follow certain distributions. Of course, this depends on the key distribution and sometimes on the design of the hash table, but a safe assumption is that a good function should produce a uniform distribution for all possible keys.
There are no strict criteria for defining “quality” but there are many widely used and agreed-upon tests to evaluate it. For example, these tests may check the distribution of values within small bit ranges of the hash results (e.g., since small portions of hashes are often used in Swiss hash tables or in extendible hash tables), or how the output changes when only a single bit in the input key is flipped (the so-called avalanche test).
Several open-source tools exist for testing hash functions, such as Appleby SMHasher or DemerPhq SMHasher. The most rigorous one, however, is Rurban SMHasher. If your hash function passes these tests, congratulations — your function is of high quality. But even if it does not, the function may still be useful, as many well-known hash functions in practice do not pass all tests.
-
Strength. Like cryptographic functions, hash functions used in hash tables should also be relatively strong. In other words, finding different keys that produce the same hash during program execution should be a difficult problem. If the hash function is weak and, for example, used in a web service, an adversary could generate many different keys with identical hashes, causing the hash table to degrade to quadratic complexity and significantly slowing down the service. In other words, weak hash functions open the door to denial-of-service attacks. A well-known example is an old Ruby vulnerability.
-
Portability. For wide adoption, a hash function should be portable. This includes both the implementation language and the primitives used in its calculation. For example, a hash function implemented in assembly may be faster than the same function written in C, since even the best C compilers can spill intermediate values to memory, which can considerably slow down hashing. However, assembly implementations are difficult to use and even harder to port across platforms.
Hash functions also rely on different primitives for their implementation. Some of these primitives may be practically non-portable, such as the AES instructions available on x86-64 processors. While the AES instructions can be leveraged for very fast hashing, they are not universally supported and therefore limit portability.
-
Simplicity. Implementations of hash functions vary widely, from just a few lines of source code to several thousand. Large implementations are typically designed for maximum speed and often include a set of different hash functions optimized for different key length ranges. Smaller hash functions, all else being equal, are easier to work with — to understand, port, debug, and maintain.
-
Stability. This means producing the same hash for the same key regardless of conditions such as architecture or key alignment. While this requirement is not critical for the performance of hash tables, it simplifies tasks like debugging. Moreover, there are other use cases for non-cryptographic hash functions where stability is essential — for example, when calculating checksums of files.
As you can see, designing a good hash function is the art of maneuvering between different, sometimes contradictory, requirements.
The priorities for cryptographic hash functions are different: their top priority is strength, and they may also include additional requirements, such as ensuring that hashing different keys takes the same number of CPU cycles.
MUM-based Hash
Hash functions are built from a variety of primitives and building blocks. Sometimes these primitives are simple machine instructions, such as xor, add, shifts, and multiplies, or more specialized instructions, like AES instructions. Primitives can be combined to form larger building blocks, such as the sip-round in the well-known SipHash, which is constructed from a small set of basic primitives. In many cases, however, hash functions are composed of an ad hoc set of primitives.
Simple primitives often have low latency and can be efficiently parallelized on modern superscalar CPUs. A typical example is SipHash, which relies on add, xor, and rotate instructions.
I have considered many primitives and building blocks over the years,
and about ten years ago I believe I discovered one with particularly
good properties. It is an N*N -> 2N multiplication followed by an
add or xor of the high and low N bits. I call this building block
MUM, which stands for Multiply and Mix. For 64-bit N, MUM
would look like:
MUM64(uint64_t x, uint64_t y) uint64_t {
__uint128_t r = (__uint128_t) 0X258c4af23da09e33ULL * (__uint128_t)
return (uint64_t) (r >> 64) + (uint64_t) r
}
I might have reinvented the wheel, but I had never seen this primitive used in hash functions before. After publishing the MUM hash function, however, the primitive became popular — for example, in xxHash3, wyhash and the GO language hash, which was inspired by it.
Actually, I initially wanted to call it MUR (Multiply and Reduce), but that name was already used by Austin Appleby for his function, where it means Multiply and Rotate.
Many hash functions have used multiplication before, so it might seem
that I invented nothing new. However, previous hash functions
typically used N*N -> N multiplication and did not mix the high and
low bits of the result. Using N*N -> N instead of N*N -> 2N makes
the hash function significantly slower while achieving the same
quality.
Practically all modern architectures have very fast multipliers. While
the latency of a multiply instruction is higher than simpler
operations like add, xor, or rotate, a single multiply mixes N*N bit
pairs rather than just N bits, as xor does. On x86-64, the latency of
a multiply instruction is roughly four times that of xor or
add. However, on modern architectures, the throughput of multiply
instructions is similar to that of xor or add. This means that long
sequences of multiply instructions can execute in roughly the same
time as an equivalent number of add, xor, or rotate instructions,
making MUM-based hash functions potentially very fast.
It is also easy to achieve good quality with MUM-based hash functions. Because they mix more bit pairs than functions based solely on add, xor, or rotate, their speed and quality can be high simultaneously.
MUM-based hash functions should also exhibit good strength. It is
difficult to find a different operand that produces the same hash. As
an exercise, you can try to find an operand x for which:
MUM64(x,0X258c4af23da09e33) = 0x11d934b3c798d46d
The strength of a MUM-based hash can be further improved by using a random hash seed, as is done in many programs.
Regarding portability, practically all major architectures support
N*N -> 2N multiplication instructions for N = 64 bits. On some
architectures, like AArch64, there are two separate instructions to
generate the low and high bits of the product. If a 64-bit N*N -> 2N
instruction is unavailable, it can be implemented using three
(N/2)*(N/2) -> N instructions. MUM hash functions can also be easily
implemented using modern C standards.
With the fast MUM primitive available, it can be used to update an
internal N-bit state. The final state at the end of the hash function
becomes the hash result. Building a good hash function around this
primitive requires some additional considerations. To achieve parallel
execution of multiple MUM primitives with a small issue gap, loops
with a constant number of iterations are used. Most optimizing C
compilers unroll such loops into linear code. Essentially, instead of
for (i = 0; i < keylen_words; i++) state ^= MUM(key[i], constants[i%<number of constants>])
<tail processing>
we use
for (i = 0; i < keylen_words/8; i++)
for (j = 0; j < 8; j++) state ^= MUM(key[j], constants[j])
<word tail processing>
<tail processing>
Here constants are random with uniform distribution of 1 and 0 bits.
Since only a small number of constants are used, they are embedded as immediate operands in machine instructions, and memory is accessed only for the key.
MUM-based hash functions also employ common techniques, such as processing tails using a C switch statement and taking advantage of unaligned memory access where possible, provided that identical hash results across architectures are not required. You can see these techniques in the source file.
The consistent use of the MUM primitive keeps MUM-based hash functions simple. Compared to the widely used xxHash3, a MUM-based hash function is 3.5 times smaller in terms of source lines of code (SLOC).
Vector variant of MUM hash function
I implemented the first version of the MUM hash function almost eight years ago. Development of new hash functions by others continued after that, so to stay competitive, I created two more improved versions.
Still I noticed that many people focus heavily on optimizing hash function speed for very long keys, even though this is rarely the critical case for hash tables. I felt that this focus was a barrier to the popularization of MUM-based hashing.
Hash functions that are fastest on long keys typically rely on machine vector instructions.
At some point, I decided to improve the performance of MUM-based hash functions on long keys by incorporating vector instructions. My goal was not only to improve speed on very long keys but also to avoid complicating the hash function.
To achieve this, I added a vector computation layer to MUM-based
functions that activates when the key length is 512 bytes or
more. This layer uses 256-bit vector instructions on x86-64 and
128-bit vector instructions on AArch64 and PowerPC64. The main vector
instruction performs two or four 32-bit * 32-bit -> 64-bit
multiplications — in other words, the layer implements a vector
version of the MUM32 primitive.
For architectures other than x86-64, AArch64, and PowerPC64, I implemented vector MUM32 using scalar instructions, preserving the portability of the hash functions.
In addition to adding the vector layer, I significantly improved hashing for keys longer than 15 bytes by reducing the number of MUM64 primitives used, while still passing all SMHasher tests.
This new version is called VMUM.
Thanks to the careful implementation of the vector layer, the source lines of code (SLOC) for VMUM increased by only 45% relative to the original MUM version.
MUM hash function performance
For comparison of MUM-based hash functions, I selected the fastest high-quality hash functions based on speeds measured by SMHasher.
Below are my measurements of speed, relative to VMUM, for different key lengths on an AMD Ryzen 9900X.
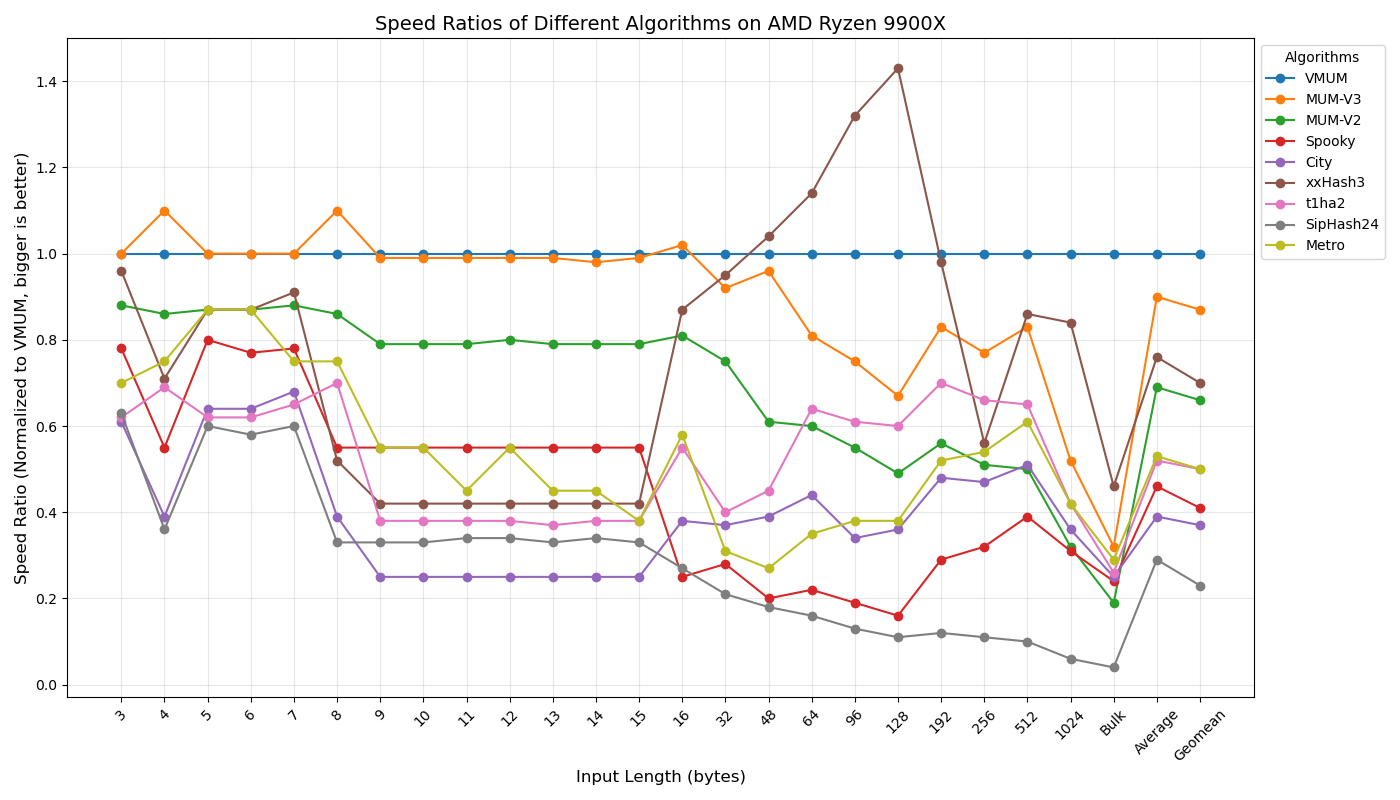
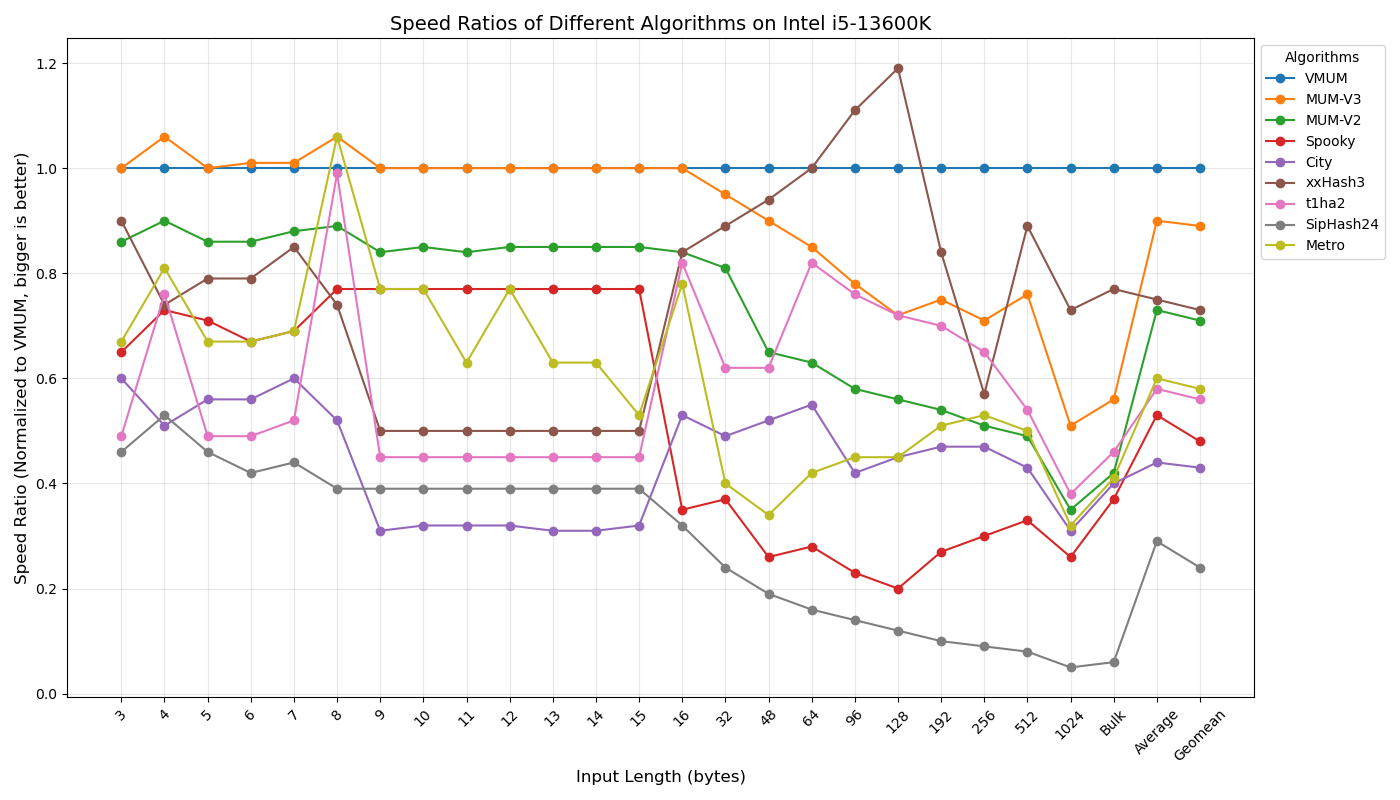
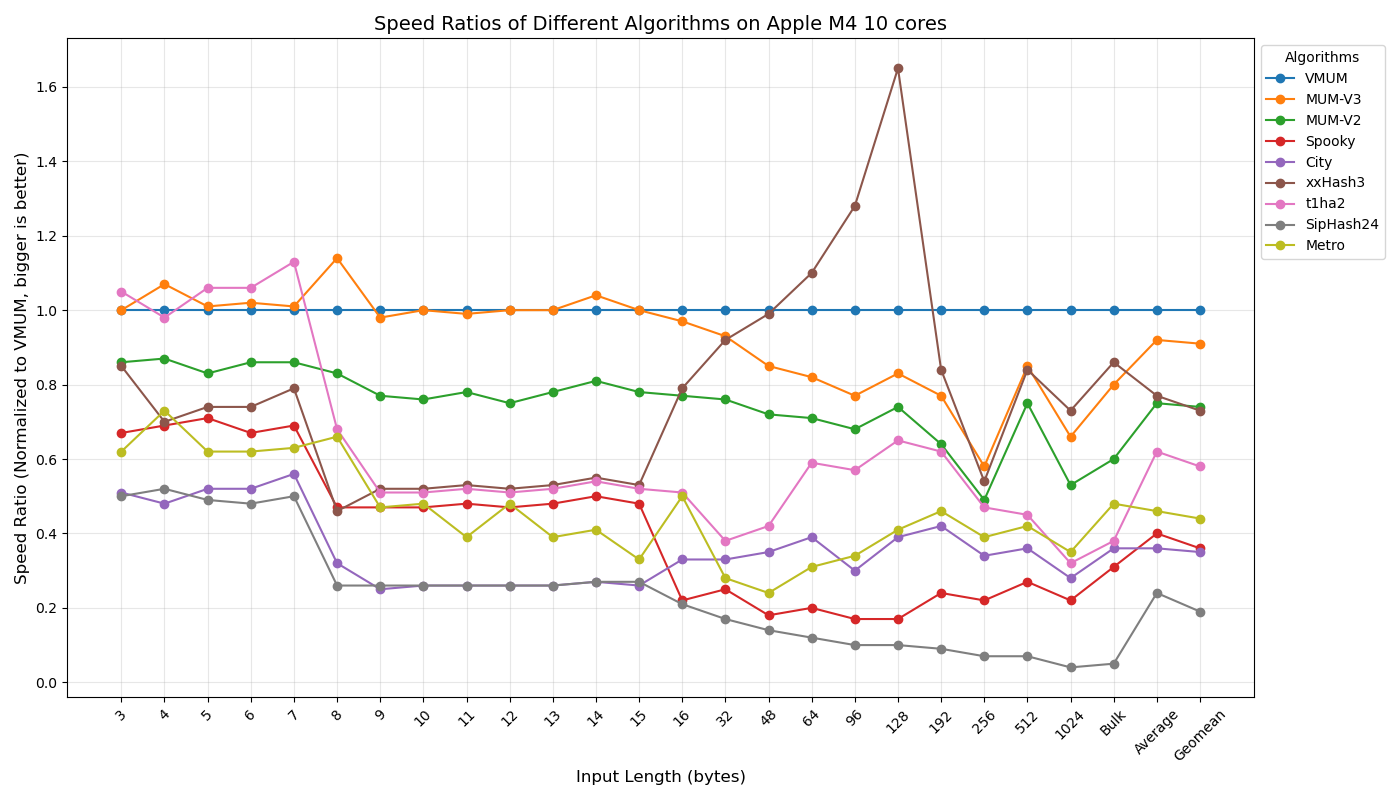
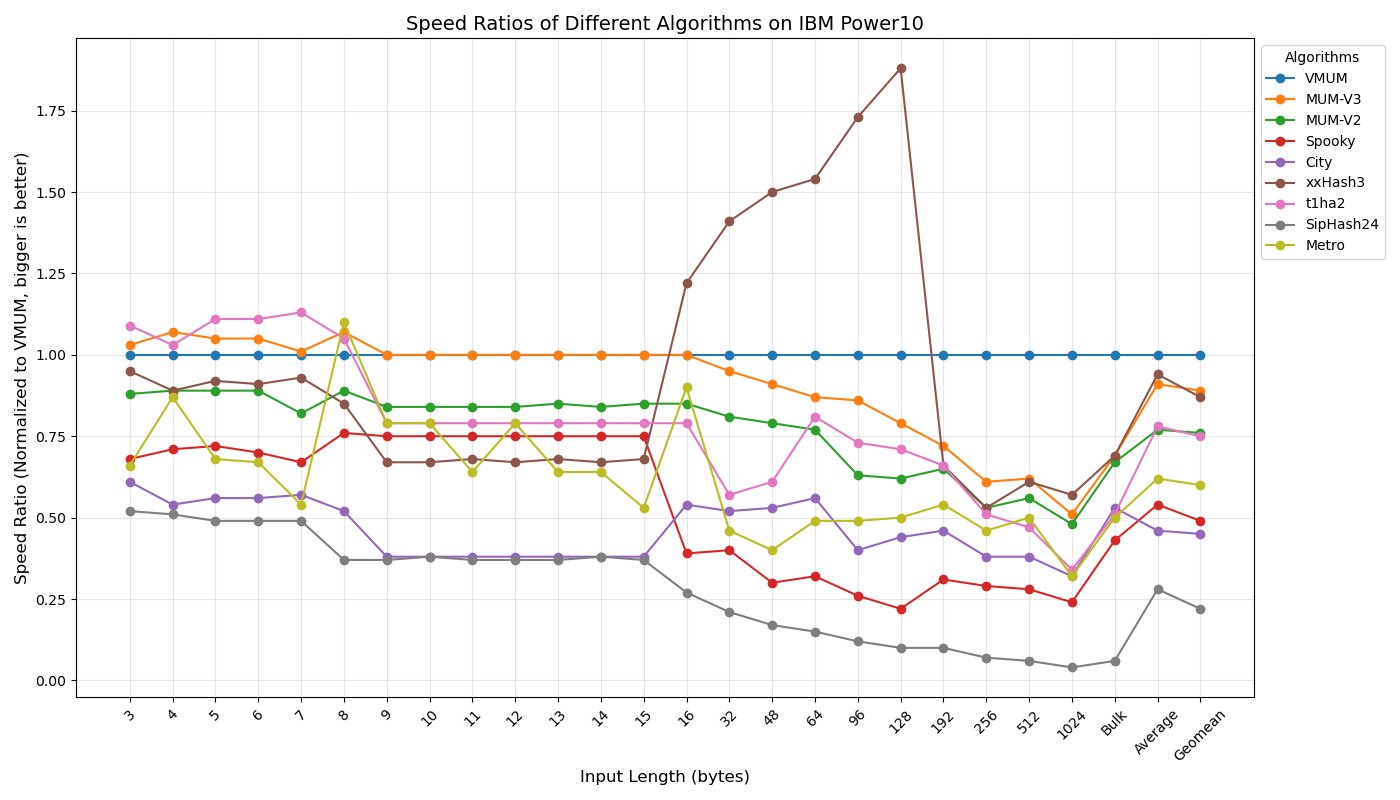
Again, for me, speed on short keys is the most important, since optimization passes in the compilers I work with mostly use hash tables with short keys (1–4 machine words). In this scenario, MUM-based hash functions are unbeatable.
I suspect that the fast-running SMHasher speed tests may sometimes produce inaccurate results. For this reason, I prefer my own long-running benchmarks. Still, for those interested in SMHasher results on the AMD Ryzen 9900X, here they are:
| Hash | AES | Bulk Speed (256KB): GB/s | Av. Speed on keys (1-32 bytes): cycles/hash | SLOC |
|---|---|---|---|---|
| VMUM | - | 143.5 | 16.8 | 411 |
| MUM | - | 39.5 | 16.1 | 284 |
| xxh3 | - | 66.6 | 17.6 | 965 |
| umash64 | - | 63.1 | 25.4 | 1097 |
| FarmHash32 | - | 39.8 | 32.6 | 1423 |
| wyhash | - | 39.3 | 18.3 | 194 |
| clhash | - | 38.4 | 51.7 | 366 |
| t1ha2_atonce | - | 34.7 | 25.5 | 2262 |
| t1ha0_aes_avx2 | Yes | 128.9 | 25.0 | 2262 |
| gxhash64 | Yes | 197.1 | 27.9 | 274 |
| aesni | Yes | 38.7 | 28.5 | 132 |
Cryptographic MUM hash function
As mentioned above, it is very difficult to determine the operand of
MUM64 given the factor and the result. A brute-force approach would
require executing up to 2^64 MUM64 operations to solve the problem.
Based on this property, I decided to create a candidate cryptographic hash function that produces a 512-bit output. I call it MUM512.
The function uses a 512-bit internal state and is based on the MUM128
primitive, which relies on 128×128 → 256-bit multiplication.
Why is it only a candidate? No differential cryptanalysis has been performed, nor have the probabilities of various attacks on the hash function been investigated. The current implementation may also be vulnerable to timing attacks on systems where multiplication instruction latency varies, and no countermeasures have been implemented.
While speed is not the most important requirement for cryptographic hash functions, here is the speed of MUM512 on an AMD Ryzen 9900X, compared with SHA-2 and SHA-3 and SSE version of Blake2
| MUM512 | SHA2 | SHA3 | Blake2B | |
|---|---|---|---|---|
| 10 bytes (20 M texts) | 0.27s | 0.27s | 0.44s | 0.81s |
| 100 bytes (20 M texts) | 0.36s | 0.25s | 0.84s | 0.84s |
| 1000 bytes (20 M texts) | 1.21s | 2.08s | 5.63s | 3.70s |
| 10000 bytes (5 M texts) | 5.60s | 5.05s | 14.07s | 7.99s |
There is a significant potential to improve MUM512 speed by using vector instructions.
Random functions based on MUM
People often say that Hash functions are Cryptography’s workhorse. However, this is true for any hash function. Once you have a hash function, it is straightforward to create a pseudo-random number generator (PRNG): to generate the next pseudo-random number, simply apply the hash function to the result of the previous call.
Based on this idea, I created pseudo-random generators mum-prng.h and mum512-prng.h using MUM and MUM512 hash functions.
Because MUM-based hashes are fast, they can compete with the fastest PRNGs, such as xoroshiro. Unlike xoroshiro and GLIBC PRNGs, all MUM-based generators pass all statistical tests of PractRand on a 4 TB PRNG-generated stream, a process that takes several days. MUM and MUM512 PRNGs also pass the NIST Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications (version 2.2.1) on 1,000 bitstreams, each containing 1 million bits. This provides further confirmation of the quality of MUM hash functions.
I tested the speed of the following pseudo-random generators:
- crypto-secure Blum Blum Shub PRNG
- PRNG based on fast cryto-level hash functions in ChaCha
- PRNG based on SipHash24
- xoroshiro128+
- xoroshiro128**
- xoshiro256+
- xoshiro256**
- xoshiro512**
- GLIBC
rand()
Below is the speed of the PRNGs in millions of generated pseudo-random numbers per second:
| M prns/sec | AMD 9900X | Intel i5-13600K | Apple M4 | Power10 |
|---|---|---|---|---|
| BBS | 0.0886 | 0.0827 | 0.122 | 0.021 |
| ChaCha | 357.68 | 184.80 | 262.81 | 83.20 |
| SipHash24 | 702.10 | 567.43 | 760.13 | 231.48 |
| MUM512 | 91.54 | 179.62 | 268.04 | 44.28 |
| MUM | 1947.27 | 1620.65 | 2263.68 | 694.42 |
| XOSHIRO128** | 1797.02 | 1386.87 | 1095.37 | 477.67 |
| XOSHIRO256** | 1866.35 | 1364.85 | 1466.15 | 607.65 |
| XOSHIRO512** | 1663.86 | 1235.15 | 1423.90 | 631.90 |
| GLIBC RAND | 115.57 | 101.48 | 228.99 | 33.66 |
| XOROSHIRO128+ | 1786.62 | 1299.59 | 1296.48 | 549.85 |
| XOSHIRO256+ | 2321.99 | 1720.67 | 1690.96 | 711.41 |
| XOSHIRO512+ | 1808.81 | 1525.18 | 1659.76 | 717.12 |
On the M4, the MUM-based PRNG is the fastest. On x86-64 machines, it ranks second, and on the Power10, it is third. However, the faster PRNGs do not achieve the same statistical quality as the MUM PRNG.
Conclusion
Designing the MUM hash function required a significant investment of time, experimentation, effort, and computing resources. The final result, however, is quite satisfactory. The development of machine architectures continues, and new vector (and multiply) instructions may be added and widely adopted in the future. Consequently, I expect my work on hash functions to continue evolving alongside these advancements.